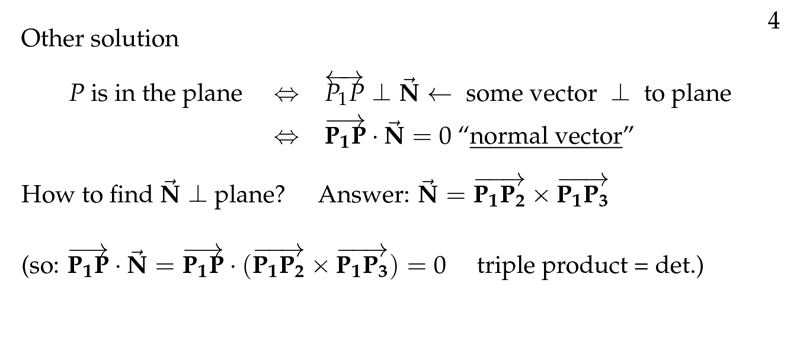Cross Product

Feb 18, 2023

• Definition
  • Cross Product is a vector
  • How to compute
• Theorem
  • Length: $|\vec{A} \times \vec{B}| = |\vec{A}| |\vec{B}| \sin{\theta}$ the area of the parallelogram they formed in space
    • direction of ($\vec{A} \times \vec{B}$) is perpendicular to the plane
  • Right-hand-rule
    • index finger change $[0, \pi]$ and thumbs up
  • Volume = area(base) x height = $|\vec{A} \times \vec{B}| \cdot \vec{A} \cdot \vec{n}$ = $\vec{A} \cdot (\vec{B} \times \vec{C})$ = determinant , where $\vec{n} = {\vec{B} \times \vec{C} \over |\vec{B} \times \vec{C} |}$ , a unit vector, the component of $\vec{A}$ in vertical direction. aka triple product
  • $\vec{A} \times \vec{B} = - \vec{B} \times \vec{A}$
  • $\vec{A} \times \vec{A} = 0$
• Application
  • The equation of the plane
    • 
    • 
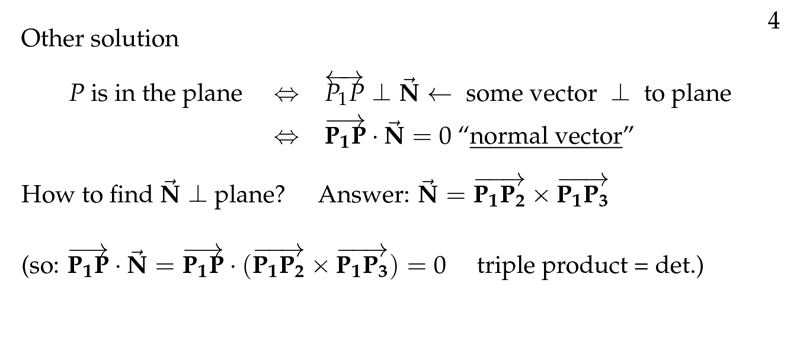
    • Find normal vector (using cross product), find P(x, y, z) , get $\vec{PP_1}$ , then $\vec{PP_1} \cdot \vec{N}$ will return the equation.