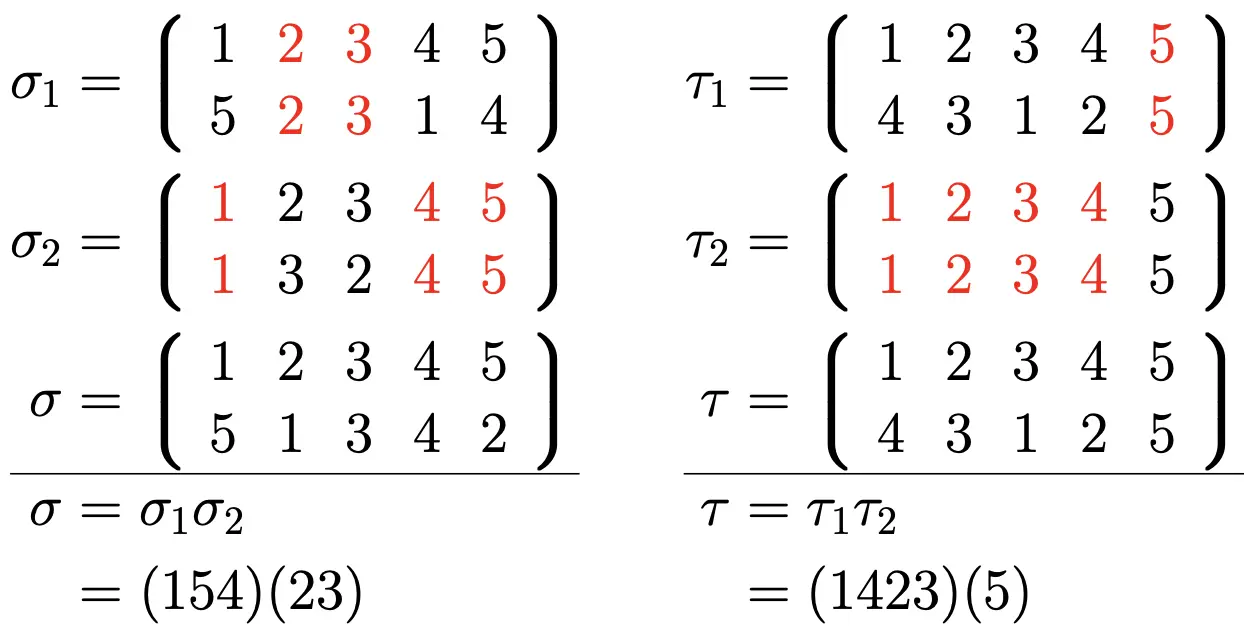Discrete Math Algebra
Jul 17, 2023
# CH9
- 交换律
- 结合律
- 消去律:消去非零元
- 吸收律:x◦(x∗y) = x 且 x∗(x◦y) = x
- 分配律:(x∗y)◦z = (x◦z)∗(y◦z) 且 z◦(x∗y) = (z◦x)∗(z◦y)
- 幂等律:xx=x
- 幺元:单位元
- 代数系统:非空集合 S 和 S 上的 k 个一元或二元运算 f1,f2,…,fk 组 成的系统称为代数系统,简称代数,记为 ⟨S, f1, f2, . . . , fk⟩。
- 子代数:
- B ⊆ S,
- B 对 f1,f2,…,fk 都是封闭的,
- B 和 S 含有相同的代数常数。
- 即证明: 运算封闭,代数常数对应。
- 子代数总是存在;
- 最大的子代数是 V 本身;
- 如果 V 中所有的 代数常数 构成的集合 B 对所有的运算 是封闭的,则 B 构成了 V 的最小子代数;
- 最大和最小子代数称为平凡的子代数;
- 若 B 是 S 的真子集,则 B 构成的子代数称为 V 的真子代数。
- 因子代数/积代数:
- 设 V1 = ⟨A,◦⟩和 V2 = ⟨B,∗⟩是同类型的代数系统,◦和∗ 为二元运算。在集合 A × B 上定义如下的二元运算 • :∀⟨a1, b1⟩, ⟨a2, b2⟩ ∈ A × B, ⟨a1,b1⟩ • ⟨a2,b2⟩ = ⟨a1 ◦ a2,b1 ∗ b2⟩,称 V = ⟨A×B,•⟩为 V1 和 V2 的积代数,记为 V1 ×V2。这 时也称 V1 和 V2 为 V 的因子代数。
- 即第一个数来自第一个集合,第二个数来自第二个集合,两组集合内的积,分别按照集合定义得运算运算,得到新的积
- 保持交换律 (结合律,幂等律)
- 保持零元
- 保持可逆和逆元
- 不保持消去律。
- Isomorphism
# CH10
- 半群:符合二元运算且可结合
- 设 V = ⟨S, ◦⟩ 是代数系统,◦ 为二元运算,如果 ◦ 是可结合的,则称 V 为半群;
- 幺半群或独异点:有单位元的半群
- 设 V = ⟨S,◦⟩是半群,如果 e ∈ S 是关于◦运算的单位元,则称 V 是幺半群或独异点。有时也将独异点记 为 V = ⟨S,◦,e⟩;
- 群:有单位元,可结合,有逆元
- 设 G 为有限群,$a \in G$,则 $a=a^{-1}$ 当且仅当 a 为一阶元或二阶元。
- 设 G 为有限群,则 G 中阶大于 2 的元素有偶数个。
- 置换群:双射 S -> S
- 对称群:所有 n 元置换构成的集合 S,有 3! 个
- 轮换:σ(i1) = i2,σ(i2) = i3,…,σ(ik−1) = ik,σ(ik) = i1 (1 < k < n), k 阶轮换,(i1, i2, . . . , ik)
- 对换:k = 2
- 子群格:设 G 为群,令 S = {H | H 是 G 的子群} 是 G 的所有子群的 集合,在 S 上定义如下关系 R: ∀A, B ∈ S, ARB ⇔ A 是 B 的子群 则 ⟨S, R⟩ 构成偏序集,成为群 G 的子群格。
- Group
- Coset
- Ring
# CH11
格和布尔代数