GCD
# Divisor
A divisor of n, also called a factor of n, is an integer m that can be multiplied by some integer to produce n.
and n is a multiple of m.
$n = km$ then $m | n$
# GCD
Greatest common divisor. It is also termed as the highest common factor (HCF) or the greatest common factor (GCF).
Euclidean algorithm - Wikipedia
# Properties
- $gcd(a, b) = ar + bs$ Bezout’s Identity
- If $gcd(a, n) = 1$ and $gcd(a, m) = 1$ then $gcd(a, mn) = 1$
- Lamé’s Theorem:
- If Euclid’s Algorithm requires
ksteps to compute thegcdof some pair, then the smaller number in the pair must be greater than or equal to thekthFibonacci number. - $n \geq Fib(k) ≈ \frac{\phi^k}{\sqrt{5}}$, order of growth is $\Theta(\log n)$
nis the smaller of the two inputs to the procedurekis the number of steps taken by the process
- If Euclid’s Algorithm requires
# Method 1: Prime Factorizations
to compute $gcd(48, 180)$, we find the prime factorizations $48 = 2^4 \cdot 3^1$ and $180 = 2^2 \cdot 3^2 \cdot 5^1$; the GCD is then $2^{min(4,2)} · 3^{min(1,2)} · 5^{min(0,1)} = 2^2 · 3^1 · 5^0 = 12$
I Do Maths · Prime Numbers and Prime Factorization
# Method 2: Euclidean Algorithm
The Euclidean Algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number.
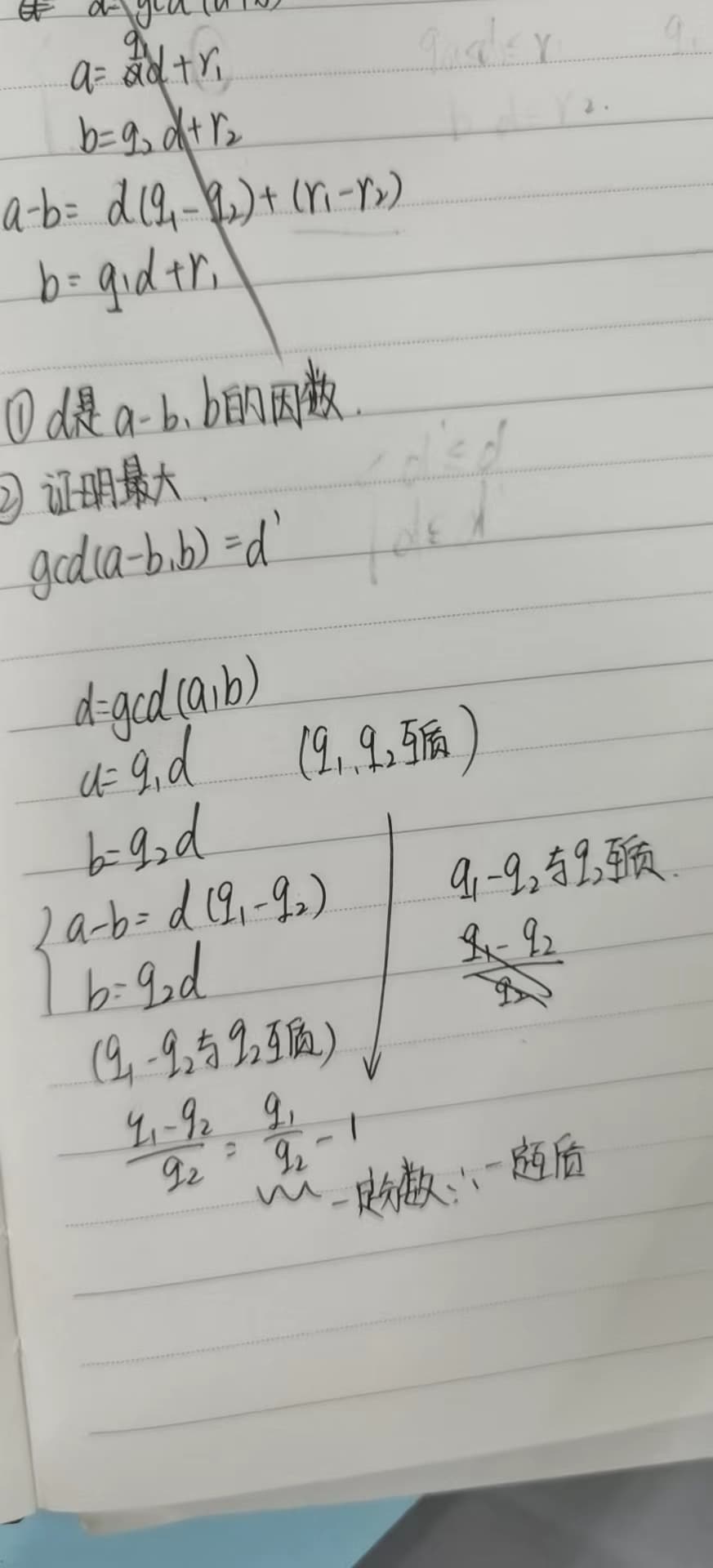
# Code for GCD
int gcd(int a, int b)
{
if (b == 0)
return a;
else
return gcd(b, a % b);
}
- gcd(0, v) = v, because everything divides zero, and v is the largest number that divides v. Similarly, gcd(u, 0) = u.
- gcd(2u, 2v) = 2 · gcd(u, v)
- gcd(2u, v) = gcd(u, v), if v is odd (2 is not a common divisor). Similarly, gcd(u, 2v) = gcd(u, v) if u is odd.
- gcd(u, v) = gcd(|u − v|, min(u, v)), if u and v are both odd.